WE find among the earliest bivalves of the Silurian system the delicate Terebratula, with its punctured umbone; we follow it downwards through all the various formations, and see it appearing on each succeeding stage, specifically new, but generally old, until, quitting the rocks with their dead remains, we pass to the existing testacea of our seas, and find among them the ancient Terebratula still extant as a living shell. Contemporary as a genus with every extinct form of animal life, we find it contemporary with the last of created

[308 APPENDIX.]
 
beings also, — contemporary with ourselves; and the Terebratula is but one existence of a class to which, though their generic antiquity may be rather less remote, nearly the same remark applies. The ostrea still exists, — its congener and contemporary the gryphæa has perished; the nautilus survives, — its congener and contemporary the ammonite is long since dead; the cuttle-fish abounds on our shores, — its congener and contemporary the belemnite is to be found in only our rocks. And thus the list runs on. We can scarce glance over a group of fossils, whatever its age, which we do not find divisible into two classes of types, — the types which still remain, and the types which have disappeared. But why the one set of forms should have been so repeatedly called into being, and why the other set should have been suffered to become obsolete, we cannot so much as surmise. Why, it may be asked, should the nautilus continue to exist, and yet the ammonite have ceased with the ocean that deposited the Chalk? or why should we have cuttle-fish in such abundance, and yet no belemnites? or why should not the gryphæa have been reproduced in every succeeding period with the oyster? In visiting some old family library, that has received no accessions to its catalogue for perhaps more than a century, one is interested in marking its more vivacious classes of works, — its Spectators, and Robinson Crusoes, and Shakespeares, and Pilgrim's Progresses, in their first, or at least earlier editions, ranged side by side with obsolete, long-forgotten volumes, their contemporaries, that died on their first appearance, and with whose unfamiliar titles one cannot connect a single association. But it is always easy to say why, in the race of editions, the one class should have been arrested at the very starting-post, and why the other should have gone down to be contemporary with every after production of authorship, until the cultivation of letters shall have ceased. It is otherwise, however, with the geologist. He finds he has exactly the same sort of fact to deal with, —

[APPENDIX. 309]
 
an immense multiplication of editions, in the case of some particular type of fish, or plant, or shell, and in the case of other types, no after instances of republication; but he finds himself wholly unable to lay hold of any critical canon through which to determine why the one class of types should have been so often republished, or the other so peremptorily suppressed. And yet, were all the circumstances known, it is possible that some such canon might be found to exist. Geology is still in its infancy. Shall a day ever arrive when, in a state of full maturity, it will be able to appeal to its fixed canons, and to say why one certain type of existence was fitted for but one definite stage in the pro gress of things, and some other certain type fitted, by a peculiar catholicity of adaptation, for every succe eding period?
 

SIR DAVID BREWSTER ON THE CUTTLE-FISH AND BELEMNITE.

THE following discovery of Sir David Brewster, regarding a marked peculiarity of structure in the eye of the cuttle fish, now first made public, will be deemed of great interest by all who have learned to admire that inconceivable variety of design in the works of the Infinite Mind which grows upon the inquirer the more he examines, and which, if man were not immortal, it would be an error of his very nature to have the strong existing desire to examine: —

MY DEAR SIR, — I have been reading, with great pleasure, your interesting account of the cuttle-fish, and was glad to find that you had noticed the singular structure of its eye. During the last twenty years I have dissected literally hundreds of cuttle-fish eyes, but I never published my observations on them, in consequence of having found singular discrepancies in the eyes of different species, and having been

[310 APPENDIX.]
 
always expecting from America the eyes of the remarkable varieties which occur there, and which have been repeatedly promised me by American naturalists.

As you will take a great interest in the subject, I shall endeavour to give you some idea of what I have done.

Independent of the peculiarity which you have noticed, of there being no aqueous chamber between the cornea and the lens, there is no iris and no pupil the quantity of light admitted being regulated by the eyelids.

The lens itself is of a most singular description. It consists of two lenses sticking together, and capable of being separated without injuring either. This structure is unique.

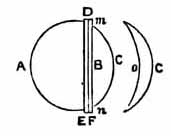
The lens D A E C consists of two, D A E, and a meniscus, m C n, which is kept close to D A C by a double cartilaginous ring, D E. The dimensions are D E =  0.51 inch, A C = 0.433 inch, A B = 0.3433 inch, B C = 0.09 inch; m n = 0.333 inch. The outer diameter of the front ring, D F, is = 0.59 inch, and its inner diameter = 0.31 inch.

In some indurated lenses I find the lens C to be doubly convex, and the surface of the lines D E A, on which it rests, concave. This must have been the lens of a different species.

The fibrous structure of the lens is very remarkable. The laminæ, or coats, of the lens are parallel to D A E and m C n; and the fibres of the lens D A E diverge from A as a pole, like the meridians of a globe; and they all terminate, not in another pole, but in the surface D E, or that which corresponds with m o n. This termination of the whole component fibres of the lens D A E in a surface is quite unique, and the mode of converting this rough plane (like a shaving-brush cut across), into a smooth surface, is singularly beautiful. Each elementary coat, or lamina, being composed of fibres, has at its termination in the periphery

[APPENDIX. 311]
 
D E a sort of selvage, where all the fibres end; and these selvages, being circles, fill up, as it were, or compose the flat surface of the lens.

The coats, or laminæ, consist of'fibres different from those of all other animals. When other lenses harden, they form a solid body, transparent like a gum; but the cuttle-fish retains its laminated structure, and shines with all the brilliancy of a pearl.

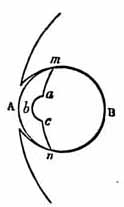
In the Sœpia Electona the front lens A separates from B in the line m a b c n, a peculiarity which I have never found in the  Sœpia Loligo. The diameter A B is larger than m n.

It would be curious to find the lenses in a fossil state.

I have found some lenses of the Sœpia Loligo of a paraboloidal form. It is probable that the form of the lens varies with the age of the animal.

When the lenses become indurated, they often exhibit the most beautiful internal reflections, and I have often thought of having them set as brooches. The pearly structure is produced by long exposure under ground; and it is almost impossible to distinguish such lenses from pearls when the convex part only is shown. — I am, my dear Sir, ever most truly yours,

 
To HUGH MILLER, Esq.

[312 APPENDIX.]
 

THE mean level of the sea cannot be regarded as a fixed line, unless, during the geologic changes of the past, it has invariably maintained the same distance from the earth's centre. If the earth, in consequence of the expansive influence of a vastly higher temperature than that which in the present era it possesses, was once greatly bulkier than it is now, the line, in proportion to the bulk, would be further removed than it is now from the centre. The sea would stand greatly higher than at its present line. And who that has surveyed the contortions, the bends, the inflections, the ever-recurring rises and falls, of the more ancient stratified rocks, such as our Scotch grauwacke for instance, — bends and inflections that forcibly remind the geologist of the foldings of a loose robe, grown greatly too large for the shrunken body which it covers, — or that has weighed the yet further evidence furnished by the carboniferous vegetation, extra-tropical in character even in Greenland, — who, I say, that has considered this evidence will venture to decide that the earth's temperature was not higher, nor the earth's radius greater, in the days of the Silurian period, or of the Coal Measures, than it is now? And, of course, if the earth's radius was greater, the level line of the sea must have stood higher,— vastly higher, it seems not impossible,

[THEORY OF THE OCEAN'S LEVEL. 313]
 
than the line now touched by the summits of our highest mountains. Had there been a graduated pole of adamant, equal in length to the radius of the globe, placed in that ocean of the Silurian period in which our Scotch graptolites lived, — a pole with its lower end fixed immoveably at the earth's centre, and its upper end level with the medium surface of the sea, — where, I marvel, would that upper end be now? High, I suspect, in the clouds; nay, in an attenuated atmosphere, to which cloud never now ascends. The graduated markings of the pole, indicatory not merely of how the tide, but also of how the land has fallen, would, I doubt not, be found more conveniently summable in leagues than in fathoms.

But even setting aside all this as fanciful and extravagant, — even taking it as a given fact (what, I suspect, is no fact at all) that the earth's bulk has not very materially altered, the line of the sea-level may have, notwithstanding, been considerably affected simply by the rise of the land. It is estimated that about one-fourth part of the surface of the globe is occupied, according to the present distribution of oceans and continents, by land, and the remaining three-fourths by water; or, more correctly, that the land is as 1, and the water as 2.76. Let us suppose this fourth part of land annihilated to the mean depth of the ocean. Of course, the effect would be, that the ocean, having then to cover four parts, instead of three, would sink, all over the globe, exactly one-fourth part of its mean depth. If the mean depth of the ocean be, as has been estimated, four miles, the fall in its level that would take place, in consequence of this annihilation of the land, would be just a single mile. And, of course, a creation of land at the bottom of the sea, which would rise to its surface, would, on the same principle, and in exactly the same ratio, have the effect of elevating the ocean level. It would do on a large scale what the pebbles dropped by the crow in the fable

[314 APPENDIX.]
 
into the pitcher did on a small one. Nor must it be for gotten, that though creation and aunihilation are terms which may seem suggestive of the fanciful and the extravagant, there are phenomena exceedingly common in nature which, for all the purposes of my argument, would have exactly the effect of the things which these terms signify. In intense cold, the mercury in a thermometer is confined to the bulb of the instrument; plunged into boiling water, it straightway rises 212 degrees in the tube; and, when a second time subjected to the intense cold, it sinks again into the bulb as at first. So far as mere bulk is concerned there takes place what is analogous to a creation and annihilation of the quantity of mercury in the tube. Again, if a rod of lead a mile in length be raised in temperature from the freezing point to the point at which water boils, it lengthens rather more than five yards; — what is equal to a creation of five yards of lead-rod has been effected. Cooled down again, however, the five yards are annihilated. A rod of flint-glass of the same length, raised to the same temperature, would stretch out only four feet two inches and rather more than seven lines. All the metals — even platinum — expand more than glass; but were there some deep-lying stratum, five miles in thickness, of that portion of the earth's crust on which Great Britain rests, to be heated 212 degrees above its present temperature, it would at even this comparatively low rate of expansion elevate the island more than twenty feet higher than now over the existing sea-level, — a height fully equal to that of by far the best marked of our ancient coast lines. And if this increase in temperature took place, not in a stratum of the earth's crustfve miles in thickness, underlying Great Britain, but in a stratum twenty miles in thickness, underlying one-fourth the area of the bed of the ocean, the effect would of course be of a reverse character. This creation of land at the bottom of the sea would raise the ocean level nearly twenty feet all over the

[THEORY OF THE OCEAN'S LEVEL. 315]
 
globe, and send the waves dashing around our own shores, against the ancient coast line, as of old.

Nor do I see that the bearing of these consequences on the sea-line, — consequences that would render its level dependent on the elevation or submergence of every continent that has existed, or shall yet exist, — can be set aside, save on the supposition that for every tract of land that rises, another tract of the same area and cubic contents sinks; or, to state the case in other words, and more definitely, that for every protuberance formed within the sea, there is a corresponding hollow formed also within it elsewhere. Now, even were it to be granted that for every protuberance which rises on the earth's crust there is a corresponding depression of the surface, which takes place somewhere else (though on what principle this should be granted is not in the least obvious), I do not at all perceive why that depression should always take place within the sea. It may take place not on any of the three parts of the earth's surface covered by water, but on that fourth part occupied by land. It may take place on the table-land of a continent. Or, vice versa, a hollow formed in the sea, considerable enough to lower the sea's level, may find its counterbalancing protuberance in the further elevation of the interior of some vast tract, such as Asia or New Holland, already raised over the ocean. The submerged continent of the Pacific, which now exists but as a wilderness of scattered atolls, may have been contemporary with that of South America, existing at the time as a flat tract, which simply occupied a certain area in the sea; and the hollow which the submergence of the Polynesian land occasioned may possibly have been balanced by the rise of those enor mous table-lands of Mexico and the adjacent countries that give to the entire continent in which they are included a mean elevation of more than a thousand feet: or the submergence of that Atlantis which was drained by the

[316 APPENDIX.]
 
great rivers of the Wealden period may have been balanccd, in like manner, by the rise of the still more extensive table-land of Asia: and in both cases the level of the sea could not fail to be very sensibly lowered. It would have in each instance the area of the submerged continent to occupy:

and there would be no corresponding elevation within its bed; to balance against the waste by the space which it filled. But why, I repeat, the balancing theory at all? If elevations or depressions can, as has been shown, be mere results of changes of temperature in portions of the earth's crust, why deem it more necessary to hold that there is a refrigerating process taking place under one area, in the exact proportion in which there is a heating process taking place under another, than to hold that when the mercury is rising in the tube of a thermometer, it is sinking in some other tube attached to the instrument, but not visible? The argument, however, is one of those which can be reasoned out more conclusively by lines than by words. It will be found, too, that the lines make out not only a more conclusive, but also a stronger case.

 

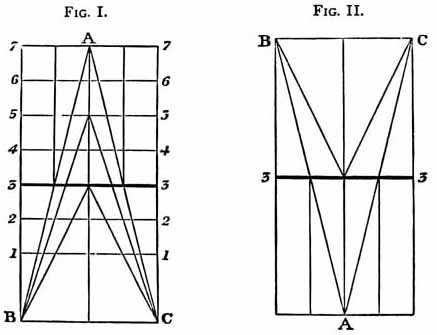
Let the line 3, 3, in the diagram, Fig. I., represent that

[THEORY OF TIlE OCEAN'S LEVEL. 317]

of the sea's mean level; the line 3 C, or 3 B, the sea's mean depth; the triangle B A C, a rising continent; and the internal triangles, whose apices reach the lines 3, 3 and 5, 5 respectively, its comparative bulk or volume during its various intermediate stages of elevation. When the rising triangle (i.e., continent) reaches the line 3, 3 (that of the sea-line ere the land began to rise), its mass, equal to that of the parallelogrammic band I B C I, shall have displaced water to that amount, and sent it to the surface, which shall have risen, in consequence, from the line 3, 3 to the line 5, 5. When the continent reaches the line 5, 5, there will be another band, equal to half the mass of the first, displaced and sent to the surface, which shall now have risen to the line 6, 6; and not until the point of the triangle (i.e., continent) has reached the line 7, 7, will it have overtaken the rising surface. Such, in proportion to its bulk, would be the effect, on the ocean-level of a rising continent, were there to be no equivalent sinking of the surface elsewhere, — just as, when the mercury of the thermometer is rising in the tube, there is no corresponding sinking of the metal contained in the instrument elsewhere, or, even if there were an equivalent sinking, were that sinking to take place in the interior of some immense tract of table-land.

Let us now, however, turn to the diagram Fig. II., and consider whether the full realization of the fiction of sinking hollows within the sea, exactly correspondent in their cubic contents to the rising continents, would be at all adequate to preserve the hypothetical fixity of ocean surface. Let the line B, C, Fig. II. represent the bottom of the ocean, and the triangle B, A, C, a depression of the earth's crust, exactly equal in cubic amount to the rising land in Fig. I., and taking place exactly at the same time. It will be at once seen, in running over the details, that even the hypothesis of balancing hollows formed in the sea as a set-off

[318 APPENDIX.]
 

against the elevations, is wholly insufficient to establish the theory of a fixed line of sea-level. The hollow might be formed, and yet the level affected notwithstanding. Until the elevation had risen above the line 3, 3 in the diagram Fig. I., and the corresponding hollow sunk to the line 3, 3 in the diagram Fig. II., the surface-line would remain un-affected, — the water displaced by the rising eminence would be contained in the sinking hollow; but immediately as the land rose over the surface, there would be a portion of it — the sub-aërial portion — which would displace no water. The hollow, if it took place in the exact ratio of the elevation, — and such is the stipulated condition of the theory, — would receive after this point exactly double the quantity of water that the land displaced, and the line of the sea-level would fall. When the elevation would have risen to the point A of the one diagram, and the hollowing depression sunk to the point A of the other, the amount of water received over water displaced would be equal in quantity to one of the parallelogrammic bands, 1 2, 2 1, or 2 3, 3 2, Fig. I.; and the sea-level would in consequence sink to the line 2, 2. The exactly balanced hollow would fail to preserve the balance.

And so I cannot continue to hold as a first principle, that the line of the sea-level is a fixed and stable line; seeing that ere I could do so I should have to believe, first, that the earth's radius has undergone no diminution since the earliest geologic periods in which an ocean existed; second; that for every elevation which takes place on the surface of the globe there takes place a corresponding depression upon it elsewhere; third; that if the elevation takes place within the bed of the sea, the depression also takes place within the bed of the sea; and, fourth, that the elevations and depressions bear always a nicely-adjusted proportion to each other in their contents, —different at two different stages of their formation, — being up

[THEORY OF THE OCEAN'S LEVEL. 319]
 
to a certain point exactly as one to one; and after that point has been reached, exactly as one to two. And I can find no adequate grounds for believing all this. But though it be thus far from self-evident that the mean level of the ocean is a fixed line, its rises and falls must have been slight indeed compared with those of the land. There are some of the Alps more than fifteen thousand feet in height; but, if spread equally over Europe, they would raise the general surface, says Humboldt, little more than twenty-one feet. And the displaced masses of the ocean, whether occasioned by the rising or the sinking of continents, have always to be spread over a surface thrice greater than that of all the land. A displacement, however, effected by the sinking of a continent which bore as large a proportion to the ocean as that borne by the Alps to Europe, would lower the general sea-line from the mean level of by far the best-marked of our ancient coast lines to the mean level of the existing one.